Math 3226

Laboratory 1B
A Substitution Technique

You will explore a substitution technique which transforms certain differential equations into linear differential equations, which can then be solved by the method discussed in class.

1 Warm-up Exercise. Find the general solution of the following differential equations:

1. 
2. 
3. 
4. 

For t>0 consider the differential equation

This differential equation is not linear because of the term. We will now perform a substitution: we will replace y(t) in the equation by

or equivalently

We will also have to replace y'(t) by an expression containing z(t) and z'(t), using the chain rule:

Performing the substitution the differential equation (1) reads as:

Multiplying by the reciprocal of the term in front of z'(t), we obtain the linear differential equation:

2 Show that equation (3) has the solutions

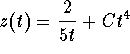
Finally we re-substitute: The solutions to the original equation (1) are given by

3 Show that the substitution transforms a differential equation of the form

into a linear differential equation (in z(t)) for !

4 Find the general solution of equation (4) for the cases n=0 and n=1.

A differential equation of the type is called a Bernoulli Equation.

5 Solve the following differential equations for the initial condition y(2)=1:

1. 
2. 
3. 

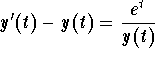
6 Solve the differential equations in 5 for the initial condition y(2)=-1. (You must slightly adapt the method for this initial condition! Why?)

7 The method of solving Bernoulli equations does not work when the initial condition is chosen so that y=0. Why? (This does not mean necessarily that a solution does not exist.) What can you say about the solutions to the differential equations in 5 satisfying the initial condition y(2)=0?