Math 3226

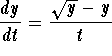
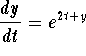
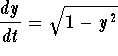
Laboratory 1D
A Substitution Technique

You will explore a substitution technique which transforms certain differential equations into separable differential equations, which can then be solved by the method discussed in class.

1 Warm-up Exercise. Find the general solution of the following differential equations. Express the solutions in explicit form, whenever possible.

1. 
2. 
3. 
4. 

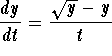
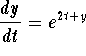
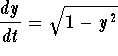
For t>0 consider the differential equation

This differential equation is neither separable nor linear. We will now perform a substitution: we will replace y(t) in the equation by

or equivalently

We will also have to replace by an expression containing z(t) and z'(t), using the product rule:

Performing the substitution on both sides of the differential equation (1) reads as:

Simplifying, we obtain the separable differential equation:

2 Show that equation (3) has the solutions

Finally we re-substitute: The solutions to the original equation (1) are given by

What is special about the differential equation (1)? It can be written in the form 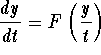, i.e. the right hand side depends only on the quotient of y and t and not on y and t independently.

3 What is this function F for the differential equation (1)?

Differential equations of the form 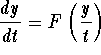are called homogeneous.

4 Show that the substitution transforms a homogeneous differential equation into a separable differential equation (in z(t))!

5 Solve the following differential equations. Express the solutions in explicit form if possible.

1. 
2. 
3. 
4. 

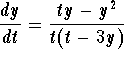
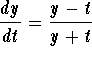
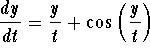
6 Investigate the slope fields of homogeneous differential equations: How can you tell from the slope field that a given differential equation is homogeneous? Hint: Find the lines on which the slope is constant.

7 Investigate the slope field of the differential equation

Using your observations in 6, explain why the differential equation is not homogeneous. Compare the slope field to the slope field of the homogeneous equation

Find a substitution method to transform the differential equation (4) into the homogeneous differential equation (5), then solve differential equation (4).