Math 3226

Laboratory 2A
Ordinary Differential Equations and World-class Sprints

According to a theory put forward by J.B. Keller, track sprints of up to 300 m can be described by the following differential equation:

where v(t) denotes the speed of the sprinter. Keller estimated the constants A and B for a (male) world-class sprinter in 1973 as follows:

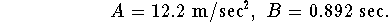
1. What is an appropriate initial value condition for the problem?

2. In your own words, explain each of the terms in the differential equation. What is an interpretation of the parameter B? Does this differential equation seem reasonable in your experience?

3. Find the sprinter's acceleration function a(t).

4. Solve the initial value problem for v(t) symbolically for general parameters A and B.

5. Find the distance function s(t) travelled in a sprint symbolically for general parameters A and B.

6. Draw a graph of the distance, velocity and acceleration functions over a reasonable interval, using the 1973 parameters.

7. When does the maximum acceleration occur, and what is it?

8. Using the 1973 parameters, how long does it take for the acceleration to drop to 10% of its maximum value?

9. What is the 1973 runner's maximal speed? In races of 100 m and 200 m, is his final speed the same? Explain!

How did Keller find the parameters A and B? In the second part of this laboratory you will address this question.

Race officials often record the split-times of runners in addition to their final times. The following table contains split-times for some sprinters during the 1993 World Championships in Stuttgart, Germany:

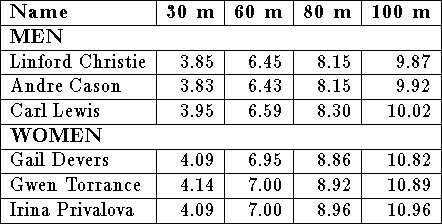
1. Using the symbolic solution you found earlier, give estimates for the parameters A and B for each of the sprinters listed. One way to do this is to first eliminate A by taking the ratios of the s(t) values, then solving for B in the resulting equation using one of the split times.

2. Graph the distance function (with the parameters A and B you obtain) for each of the sprinters, and compare it to the given split times. How good is the fit? Do you think that Keller's model describes sprints adequately?

3. Has athletic performance in 100 m sprints improved since 1973? Explain your observations!

4. Compare the parameter values A and B for men and women. Some track experts speculate that men's and women's abilities are becoming identical. Do your observations support this?

This laboratory is based on the article ``The ODE of World-Class Sprints'' by Steven R. Dunbar, which appeared in C 1#1 ODE 1#1 E, Spring 1994.

J.B. Keller,``A Theory of Competitive Running'', Physics Today, 9-1973, p. 43.

Keywords: first order linear differential equation, modeling.