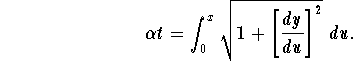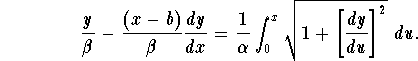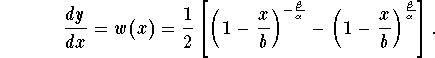Math 3226

Laboratory 2B
The Curve of Pursuit

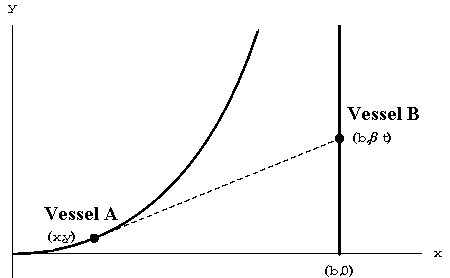
An interesting geometric problem--first considered by Leonardo da Vinci-- arises when one tries to determine the path of a pursuer chasing its prey. The simplest problem is to find the curve along which a vessel moves in pursuing another vessel that flees along a straight line, assuming that the speeds of both vessels are constant.

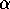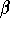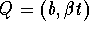Let's assume vessel A, traveling at a speed , is pursuing vessel B, which is traveling at speed . In addition, assume vessel A begins at time t=0 at the origin and pursues vessel B, which begins at the point (b,0), b>0, and travels up the line x=b. After t hours, vessel A is located at the point P=(x,y) and vessel B is located at the point . The goal is to describe the locus of points P; that is to find y as a function of x.

1. Vessel A is pursuing vessel B, so at time t, vessel A must be heading right at vessel B. Thus the tangent line to the curve of pursuit at P must pass through the point Q. For this to be true, show that

   

2. We know that the speed at which vessel A is traveling, so we know that the distance it travels in time t is 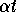. This distance is also the length of the pursuit curve from (0,0) to (x,y). Using the arclength formula, show that

   

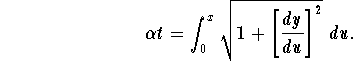
3. Solve the formulas in 1. and 2. for the variable t to obtain

   

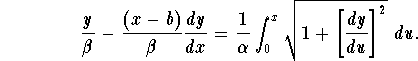
4. Set w(x)=dy/dx and differentiate both sides of the equation above with respect to x to obtain the first-order differential equation

   

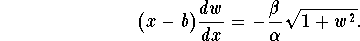
5. Using appropriate initial values for both x and w=dy/dx when t=0, show that the solution of the equation in 4. is given by

   

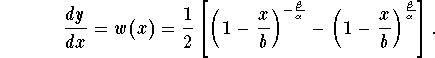
6. For the case 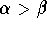, integrate the expression in 5. with respect to x to obtain y as a function of x. What is the initial condition for y when t=0?

7. For the case 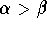, find the location where vessel A will intercept vessel B.

8. Repeat 6. for the case .

9. For the case , will vessel A ever reach vessel B?

This laboratory is based on a group project in ``Fundamentals of Differential Equations'' by R. Kent Nagle and Edward B. Saff.