Math 3226

Laboratory 2C
Aquaculture
(Prerequisite: Laboratory 1A or 1B)

Aquaculture is the art of cultivating the plants and fish indigenous to water. In the example considered here, it is assumed that a batch of catfish are raised in a pond. We are interested in determining the best time for harvesting the fish so that the cost per pound for raising the fish is minimized.

A differential equation describing the growth of fish may be expressed as

displaymath66

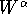where W(t) is the weight of the fish at time t, and k and tex2html_wrap_inline80 are empirically determined growth constants. The functional form of this relationship is similar to growth models for other species. Modeling the growth rate or metabolic rate by a term like tex2html_wrap_inline82 is a common assumption. Biologists often refer to the equation above as the allometric equation. It can be supported by plausibility arguments such as growth rate depending on the surface area of the gut (which varies like 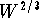tex2html_wrap_inline84 ) or depending on the volume of the animal (which varies like W).

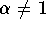  1. Solve the allometric equation for tex2html_wrap_inline88 .

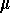  2. The solution in 1. grows large without bound, but in practice there is some limiting maximum weight M for the fish. This limiting weight may be included in the allometric equation by inserting a dimensionless variable S that can range between 0 and 1 and involves an empirically determined parameter tex2html_wrap_inline94 .

    Namely we now assume that

    displaymath67

    where S has the form

    displaymath68

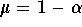    When tex2html_wrap_inline98 , this equation becomes a Bernoulli equation, and has a closed form solution. Solve the equation, when k=12, 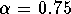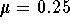tex2html_wrap_inline102 , tex2html_wrap_inline104 , M=81 ounces and W(0)=1 ounce. The constants are given for t measured in months.

  3. The differential equation describing the cost C(t) of raising fish for t months has 2 parameters: 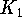tex2html_wrap_inline116 specifies the cost per month (due to costs such as interest, depreciation and labor); 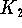tex2html_wrap_inline118 , the cost for food, multiplies with the growth rate (because the amount of food consumed by the fish is approximately proportional to the growth rate).

    That is

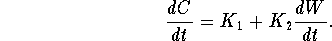
    displaymath69

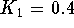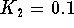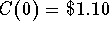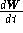    Solve this equation when tex2html_wrap_inline120 , tex2html_wrap_inline122 , tex2html_wrap_inline124 , and tex2html_wrap_inline126 as determined in 2.

  4. Explain why it is optimal to harvest the fish at the time when the ratio 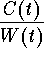tex2html_wrap_inline128 is at minimum. Estimate the optimal harvesting time to the nearest month.

This laboratory is based on a group project in ``Fundamentals of Differential Equations'' by R. Kent Nagle and Edward B. Saff.

Helmut Knaust
Mon Feb 17 20:50:55 MST 1997