Math 3226

Laboratory 2D
Modeling the Spread of a Disease
(Prerequisite: Laboratory 1A or 1B)

Suppose that a disease is spreading among a population of size N. In some diseases, like chicken pox, once an individual has had the disease, the individual becomes immune to the disease. In other diseases, like most venereal diseases, once an individual has had the disease, the individual does not become immune to the disease; subsequent encounters can lead to recurrence of the infection.

Let S(t) denote the percent of the population susceptible to a disease at time t, I(t) the percent of the population infected with the disease, and R(t) the percent of the persons who have had the disease, recovered, and have subsequently become immune to the disease.

In order to model the spread of various diseases, we begin by making several assumptions, and introducing some notation.

• Susceptible and infected individuals die at a rate proportional to the number of susceptible and infected individuals with proportionality rate 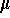, called the daily death removal rate; 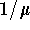is called the average life expectancy.

• The constant 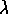represents the daily contact rate. On average, an infected person will spread the disease to 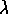people per day.

• Individuals recover from the disease at a rate proportional to the number infected with the disease, with proportionality constant 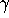. The constant 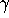is called the daily recovery removal rate; the average period of infectivity is .

• The contact number 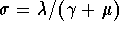represents the average number of contacts an infected person has with both susceptible and infected persons.

If a person becomes susceptible to a disease after recovering from it (like gonorrhea, meningitis and streptococcal sore throat), then the percent of persons susceptible to becoming infected with the disease, S(t), and the percent of people in the population infected with the disease, I(t), can be modeled by the system of differential equations

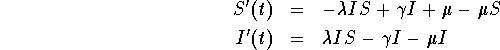
with the initial conditions , and .

1. Note that we also have S(t)+I(t)=1 for all t. Use this relationship to reduce the system to the differential equation for I(t):

   

2. Find the solution to this Bernoulli equation with the initial condition for .

3. Find the solution in the case .

4. Graph various solutions if (A) , , ; (B) , , ; in each case, find the contact number.

5. Find . How does the contact number affect I(t) for large values of t? Is there anything special about the case ?

6. The incidence of some diseases like streptococcal sore throat oscillates seasonally. To model these diseases, we will replace the constant by a periodic function .

   Graph various solutions if (A) , , and ; (A) , , and .

   In each case, calculate the average contact number. How does the average contact number affect I(t) for large values of t?

7. Explain why diseases like gonorrhea, meningitis and streptococcal sore throat continue to persist in the population. Do you think there is any way to completely eliminate these diseases from the population? Why or why not?

This laboratory is based on a group project in ``Modern Differential Equations'' by Martha L. Abell and James P. Braselton