Math 3226
Laboratory 3A
Predator-Prey Models and Hunting
Consider the classical predator-prey model

Such a system typically has a periodic solution, i.e., there is some time constant T so that
x(t+T)=x(t) and y(t+T)=y(t) for all t. Because of this periodic behavior, it is useful to consider the average populations 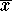 and
and 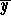 , defined by
, defined by

-
Show that
 and that
and that 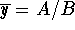 . Hint: Use the first equation above and the fact that x(0)=x(T) to show that
. Hint: Use the first equation above and the fact that x(0)=x(T) to show that

- Assume that a percentage of both species is hunted; more precisely: Assume that the prey is hunted reducing its rate of change by a constant
 times the prey population, while the predators are hunted reducing their rate of change by a constant
times the prey population, while the predators are hunted reducing their rate of change by a constant 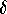 times the predator population.
Write down a system of first-order differential equations describing this new predator-prey model with hunting.
times the predator population.
Write down a system of first-order differential equations describing this new predator-prey model with hunting.
- Assume
 . What effect does this model of hunting have on the average prey and predator populations?
. What effect does this model of hunting have on the average prey and predator populations?
- Assume that only the predator is hunted. What effect does this model of hunting have on the average prey and predator populations?
- Assume that only the prey is hunted. What effect does this model of hunting have on the average prey and predator populations?
- In a rural community, foxes prey mainly on rabbits, but occasionally include a chicken in their diet. The farmers decide to put a stop to the chicken killing by hunting the foxes. What do you predict will happen?
- This laboratory is based on a group project in ``Fundamentals of Differential Equations'' by R. Kent Nagle and Edward B. Saff.
Helmut Knaust
Fri Mar 7 14:25:47 MST 1997

![]() and
and ![]() , defined by
, defined by


![]() and
and ![]() , defined by
, defined by

![]()