Math 3226

Laboratory 4C
Limit Cycles

The van der Pol equation gives an example of a system of differential equations exhibiting a limit cycle, i.e., there is a closed curve in the phase plane corresponding to periodic time series (see Figure 4.1 on page 348 of our textbook). This laboratory explores limit cycles.

Consider the following system of first-order non-linear differential equations:

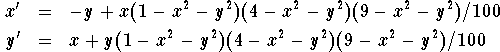
1 Classify all equilibrium points by using the technique of linearization.

2 Graph the direction field and identify all limit cycles of this system. What can you say about the shape of the limit cycles? Can you estimate the period of the corresponding time series?

A limit cycle is called attracting, if solutions nearby approach the cycle (the van der Pol equation's limit cycle is attracting!), it is called repelling if nearby solutions move away from the cycle. Last not least, a limit cycle is called semi-stable, if it is attractive for solutions from the outside and repelling for solutions from the inside, or vice versa.

3 Classify the limit cycles of the system above according to this scheme.

4 Construct a system of differential equations with two limit cycles so that the inside cycle is attractive, the outside cycle is repelling. What can you say about the character of the equilibrium points?

5 Construct a system of differential equations with two limit cycles so that the inside cycle is repelling, the outside cycle is attractive. What can you say about the character of the equilibrium points?

6 Construct a system of differential equations with one semi-stable limit cycle. What can you say about the character of the equilibrium points?

This laboratory is based on Experiment 5.15 in ``Differential Equations Laboratory Workbook" by Borelli, Coleman and Boyce.