Math 3226
Laboratory 4E
Hopf Bifurcation
A certain oscillating chemical reaction (the chlorine dioxide-iodine-malonic acid reaction) can be modeled by a system of two first-order differential equations:
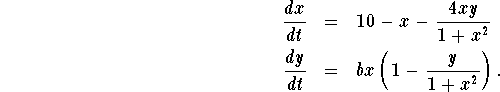
The variables x and y should be thought of as modeling concentrations of  and
and  , while b is a certain chemical constant.
, while b is a certain chemical constant.
1 Find the equilibrium point of the system above.
2 Linearize the system at the equilibrium point.
3 Let b=5. What kind of equilibrium does the system have?
4 Let b=1. What kind of equilibrium does the system have?
5 For which value of b does the system change its
equilibrium type?
6 Let b=1. Consider the rectangle

Show (using pencil and paper calculations) that no solution will leave this rectangle! Proceed as follows: show that the direction field points to the right at the left border of the rectangle, that it points to the left at the right border, that it points up at the bottom border and that it points down at the top border. Explain carefully why this establishes that no solution can escape from the
rectangle!
7 Let b=1. Describe the long-term behavior of all solutions starting inside the rectangle. Explain how you arrive at your conclusions. Hint: Look at the solutions of the van der Pol equation on page 348 of our textbook.
This laboratory is based on Experiment 25 in the ``Interactive Differential Equations Workbook" by West, Strogatz, McDill and Cantwell.
Helmut Knaust
Mon Nov 18 22:47:22 MST 1996
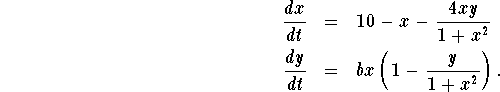
![]() and
and ![]() , while b is a certain chemical constant.
, while b is a certain chemical constant.