Finding Critical Points - CriticalPoints.nb
Finding the Critical Points
Define the function, let's say f(x), then find the solutions of f '(x)=0.
This method will obviously only find critical points, where the first derivative equals 0. Mathematica is not very helpful in finding critical points where the first derivative fails to exist.
In[1]:=
![]()
Out[1]=
![]()
In[2]:=
![]()
Out[2]=
![]()
Here is another example:
In[3]:=
![]()
Out[3]=
![]()
In[4]:=
![]()
Out[4]=
![]()
Using the Second Derivative Test
Here is our last example again:
In[5]:=
![]()
Out[5]=
![]()
In[6]:=
![]()
Out[6]=
![]()
Next, we compute the second derivative at x=-2 and at x=0:
In[7]:=
![]()
Out[7]=
![]()
Here is its numerical value:
In[8]:=
![]()
Out[8]=
![]()
In[9]:=
![]()
Out[9]=
![]()
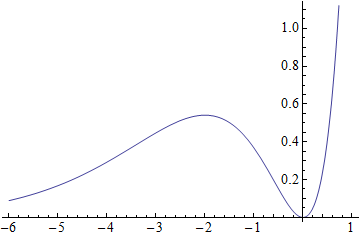
Since the second derivative is negative at x=-2, x=-2 is a local maximum; at x=0, the second derivative is positive, henceforth a local minimum occurs at x=0. Let's check this graphically:
In[10]:=
![]()
Out[10]=
The Graphical Approach
If Mathematica is unable to solve the equation f '(x)=0 algebraically, we can still graph the first derivative to estimate where it is equal to 0. Here is an example (Remember that "Log[x]" denotes the natural logarithm!)
In[11]:=
![]()
Out[11]=
![]()
In[12]:=
![]()
Out[12]=
![]()
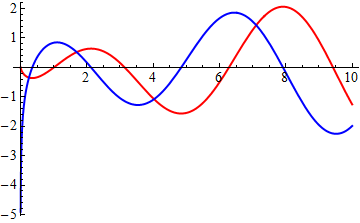
The following graph depicts f(x) in red, and f '(x) in blue, for x-values between 0 and 10. We can see that in this example critical points occur at about x=0.4, x=2.1, x=4.8 and x=7.9.
In[13]:=
Out[13]=
An Application: Snell's Law
This example refers to Chapter 5.5, Problems 21 and 22. With the notation of Figure 5.74, we have to minimize the time t(x) needed for the light ray to travel from Point A to Pint B.
t(x) is given by
In[14]:=
![]()
Out[14]=
![]()
In[15]:=
![]()
Out[15]=
![]()
It is quite hard to solve the equation t '(x)=0 for x, but if you read the problem carefully, you will see that that might not be necessary to do. Evaluate the next command only if you have some spare time to wait for the answer.
In[16]:=
![]()
Instead we will solve for ![]() :
:
In[17]:=
![]()
Out[17]=
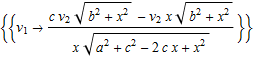
... and thus the quotient ![]() :
:
In[18]:=
![]()
Out[18]=
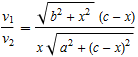
Note that the right side is indeed the quotient ![]() .
.
Why all this? We now know that the critical point satisfies Snell's Law. But is the crtitical point an absolute minimum?
Let's look at the second derivative.
In[19]:=
![]()
Out[19]=
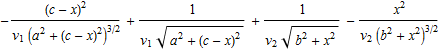
In[20]:=
![]()
Out[20]=
![]()
Written like this you can see that the second derivative will always be positive, and thus the solution given by Snell's Law is indeed an absolute minimum.
Etc.