21495: HW 3
HelmutKnaust (Talk | contribs) |
HelmutKnaust (Talk | contribs) |
||
| (One intermediate revision by one user not shown) | |||
| Line 4: | Line 4: | ||
#$A \bigtriangleup B= B \bigtriangleup A$. | #$A \bigtriangleup B= B \bigtriangleup A$. | ||
#$(A \bigtriangleup B)\bigtriangleup C=A \bigtriangleup (B \bigtriangleup C)$. | #$(A \bigtriangleup B)\bigtriangleup C=A \bigtriangleup (B \bigtriangleup C)$. | ||
| + | |||
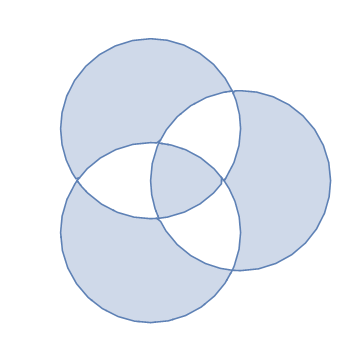
| + | [[Image:assocSSD.png|frame|center|Problem 11.2]] | ||
'''Problem 12.''' Let $A$ and $B$ be arbitrary sets. Prove or disprove the following power set relations: | '''Problem 12.''' Let $A$ and $B$ be arbitrary sets. Prove or disprove the following power set relations: | ||
Latest revision as of 16:42, 2 March 2017
Problem 11. Let $A,B$ and $C$ be arbitrary sets. Recall that $A\setminus B=\{x \ |\ x\in A\ \wedge\ x\not\in B\}$. We define $A\bigtriangleup B:=(A\setminus B)\cup(B \setminus A)$. Prove or disprove:
- $A \bigtriangleup B= B \bigtriangleup A$.
- $(A \bigtriangleup B)\bigtriangleup C=A \bigtriangleup (B \bigtriangleup C)$.
Problem 12. Let $A$ and $B$ be arbitrary sets. Prove or disprove the following power set relations:
- ${\cal P}(A\cap B)\subseteq {\cal P}(A)\cap {\cal P}(B)$.
- ${\cal P}(A)\cap {\cal P}(B)\subseteq {\cal P}(A\cap B)$.
Problem 13. Given two real numbers $a<b$, the open interval $(a,b)$ is defined to be the set $\displaystyle{\{x\in\mathbb{R}\ |\ (a<x) \wedge (x<b)\}}$.
For $n\in\mathbb{N}$, let $A_n$ be the open interval $\displaystyle{(\frac{1}{2}-\frac{1}{2n}, \frac{1}{2}+\frac{1}{3n})}$. Find $\displaystyle{\bigcup_{n\in\mathbb{N}} A_n}$ and $\displaystyle{\bigcap_{n\in\mathbb{N}} A_n}$. Confirm your conjectures by proofs.
Problem 14. Let $A$ be a set, and let ${\cal K}$ be a collection of sets. Show that \[A\cap(\bigcup_{B\in{\cal K}} B)=\bigcup_{B\in{\cal K}}(A\cap B).\]
Problem 15. Let $A$ be a proper subset of some set $U$, and let $x\in U\setminus A$. Let ${\cal B}$ consist of all sets of the form $C\cup\{x\}$ with $C\in{\cal P}(A)$, in other words \[{\cal B}=\{C\cup\{x\}\ |\ C\in{\cal P}(A)\}.\] Show that
- ${\cal P}(A\cup \{x\})={\cal P}(A)\cup {\cal B}$.
- ${\cal P}(A)\cap {\cal B}=\emptyset$.