Assignments
From Classes
(Difference between revisions)
HelmutKnaust (Talk | contribs) |
HelmutKnaust (Talk | contribs) |
||
| (6 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
# <math>\checkmark</math> Let <math>A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&10\end{pmatrix}</math>. Find a matrix X such that <math>X\cdot A=\begin{pmatrix}7&8&10\\4&5&6\\1&2&3\end{pmatrix}</math>. What do you get if you compute <math>A\cdot X</math>? | # <math>\checkmark</math> Let <math>A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&10\end{pmatrix}</math>. Find a matrix X such that <math>X\cdot A=\begin{pmatrix}7&8&10\\4&5&6\\1&2&3\end{pmatrix}</math>. What do you get if you compute <math>A\cdot X</math>? | ||
| − | # Find a 4x4 orthogonal matrix with at least 5 non-zero entries. | + | # <math>\checkmark</math> Find a 4x4 orthogonal matrix with at least 5 non-zero entries. |
| − | # Can you find a 3x3 orthogonal matrix with no zeroes? [http://helmut.knaust.info/class/201310_5311/Notebooks/Assignment03.nb Notebook] | + | # <math>\checkmark</math> Can you find a 3x3 orthogonal matrix with no zeroes? [http://helmut.knaust.info/class/201310_5311/Notebooks/Assignment03.nb Notebook] |
# <math>\checkmark</math> Find the vertical edges of a grayscale image (of your choice). Hint: For horizontal edges this is done in Notebook 031. | # <math>\checkmark</math> Find the vertical edges of a grayscale image (of your choice). Hint: For horizontal edges this is done in Notebook 031. | ||
# <math>\checkmark</math> Pick a small grayscale image (your choice) and use matrix transposition and multiplication with suitable matrices to produce the following six images: [[image:FN.jpg|500px]] | # <math>\checkmark</math> Pick a small grayscale image (your choice) and use matrix transposition and multiplication with suitable matrices to produce the following six images: [[image:FN.jpg|500px]] | ||
# In Notebook 032 you have seen how to convert a color image to its YCbCr components. Recreate the original color image from its Y-, Cb- and Cr- components. (Check your result by computing the Peak Signal to Noise Ratio to the original image. Note that when computing the luminance/chrominance components, we round to the nearest integer. ) | # In Notebook 032 you have seen how to convert a color image to its YCbCr components. Recreate the original color image from its Y-, Cb- and Cr- components. (Check your result by computing the Peak Signal to Noise Ratio to the original image. Note that when computing the luminance/chrominance components, we round to the nearest integer. ) | ||
| − | # Problem 3.8 | + | # <math>\checkmark</math> Problem 3.8 |
| − | # Problem 3.16 | + | # <math>\checkmark</math> Problem 3.16 |
# Problem 3.23 | # Problem 3.23 | ||
# Problem 3.26 | # Problem 3.26 | ||
| − | # Problem 3.35 | + | # <math>\checkmark</math> Problem 3.35 |
| − | # Problem 3.37 | + | # <math>\checkmark</math> Problem 3.37 |
| − | # Problem 3.40 | + | # <math>\checkmark</math> Problem 3.40 |
| − | # Problem 3.42 | + | # <math>\checkmark</math> Problem 3.42 |
| − | # Compute the real and/or complex Fourier series for the functions <math>f(t)=t</math> or <math>f(t)=|t|</math>. | + | # <math>\checkmark</math> Compute the real and/or complex Fourier series for the functions <math>f(t)=t</math> or <math>f(t)=|t|</math>. |
| − | # In Notebook 031 a "resampling" algorithm is shown that cuts the number of rows and columns of an image in half. Suppose you want to reduce the number of rows and columns of an image by 20%. The straightforward idea is to delete every fifth row and column, but this leads to unsatisfactory results. Can you come up with an idea and implementation for an improved algorithm that may lead to better results? It may be advantageous to first think about this problem in one dimension (for a vector). | + | # In Notebook 031 a "resampling" algorithm is shown that cuts the number of rows and columns of an image in half. Suppose you want to reduce the number of rows and columns of an image by 20%. The straightforward idea is to delete every fifth row and column, but this leads to unsatisfactory results (see below). Can you come up with an idea and implementation for an improved algorithm that may lead to better results? It may be advantageous to first think about this problem in one dimension (for a vector).<br>[[image:Lehmer01.png|400px]] [[image:Lehmer02.png|400px]] |
| + | # <math>\checkmark</math> Handout Exercise 1 | ||
| + | # <math>\checkmark</math> Handout Exercise 2 | ||
| + | # <math>\checkmark</math> Handout Exercise 3 | ||
| + | # <math>\checkmark</math> Handout Exercise 4 | ||
| + | # Handout Exercise 5 | ||
| + | # <math>\checkmark</math> Handout Exercise 6 | ||
| + | # <math>\checkmark</math> Problem 4.33 | ||
| + | # Problem 4.34. Problem 4.34(b) seems to be wrong - try <math>\overline{c_k}</math> instead. | ||
Latest revision as of 07:33, 20 June 2013
- \(\checkmark\) Let \(A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&10\end{pmatrix}\). Find a matrix X such that \(X\cdot A=\begin{pmatrix}7&8&10\\4&5&6\\1&2&3\end{pmatrix}\). What do you get if you compute \(A\cdot X\)?
- \(\checkmark\) Find a 4x4 orthogonal matrix with at least 5 non-zero entries.
- \(\checkmark\) Can you find a 3x3 orthogonal matrix with no zeroes? Notebook
- \(\checkmark\) Find the vertical edges of a grayscale image (of your choice). Hint: For horizontal edges this is done in Notebook 031.
- \(\checkmark\) Pick a small grayscale image (your choice) and use matrix transposition and multiplication with suitable matrices to produce the following six images:
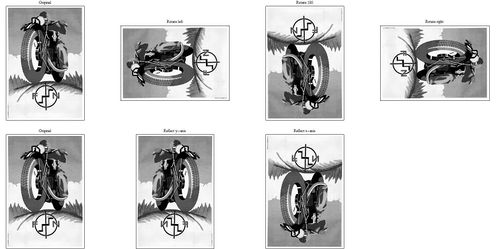
- In Notebook 032 you have seen how to convert a color image to its YCbCr components. Recreate the original color image from its Y-, Cb- and Cr- components. (Check your result by computing the Peak Signal to Noise Ratio to the original image. Note that when computing the luminance/chrominance components, we round to the nearest integer. )
- \(\checkmark\) Problem 3.8
- \(\checkmark\) Problem 3.16
- Problem 3.23
- Problem 3.26
- \(\checkmark\) Problem 3.35
- \(\checkmark\) Problem 3.37
- \(\checkmark\) Problem 3.40
- \(\checkmark\) Problem 3.42
- \(\checkmark\) Compute the real and/or complex Fourier series for the functions \(f(t)=t\) or \(f(t)=|t|\).
- In Notebook 031 a "resampling" algorithm is shown that cuts the number of rows and columns of an image in half. Suppose you want to reduce the number of rows and columns of an image by 20%. The straightforward idea is to delete every fifth row and column, but this leads to unsatisfactory results (see below). Can you come up with an idea and implementation for an improved algorithm that may lead to better results? It may be advantageous to first think about this problem in one dimension (for a vector).


- \(\checkmark\) Handout Exercise 1
- \(\checkmark\) Handout Exercise 2
- \(\checkmark\) Handout Exercise 3
- \(\checkmark\) Handout Exercise 4
- Handout Exercise 5
- \(\checkmark\) Handout Exercise 6
- \(\checkmark\) Problem 4.33
- Problem 4.34. Problem 4.34(b) seems to be wrong - try \(\overline{c_k}\) instead.