2013NREUP
From Classes
(Difference between revisions)
HelmutKnaust (Talk | contribs) (Created page with "=Summer Research Experience for Undergraduates= *Project Director: Helmut Knaust *Project Description: Five undergraduate students majoring in Mathematics will participate in ...") |
HelmutKnaust (Talk | contribs) (→Materials) |
||
| (51 intermediate revisions by one user not shown) | |||
| Line 1: | Line 1: | ||
| − | =Summer Research Experience for Undergraduates= | + | <font size=4>UTEP Summer Research Experience for Undergraduates: Applications of Discrete Wavelet Transformations</font><br><br> |
| − | *Project Director: Helmut Knaust | + | <font size=3>June 10 - July 19, 2013</font> |
| − | *Project Description | + | |
| − | The | + | |
| − | algorithm [1] can be adapted to other classes of similar images such as facial portraits. Historically | + | |
| − | the adoption by the FBI of a compression algorithm for storing fingerprints digitally was the | + | ===Program Description=== |
| − | + | [[image:MAA_logo.jpg|left]]The [http://www.maa.org/programs/faculty-and-departments/underrepresented-groups/nreup National Research Experience for Undergraduates Program (NREUP)] is a program of the ''Mathematical Association of America'', funded by the ''National Security Agency'' (H98230-13-1-0270) and the ''National Science Foundation'' (DMS-1156582). | |
| − | the general JPEG2000 compression algorithm, but cleverly exploits the special character of the | + | |
| − | images to be processed by selecting a particular wavelet package and quantization scheme, thereby | + | The target audience for the program are primarily sophomores and juniors majoring in Mathematics. Successful completion of Calculus II is required; successful completion of Matrix Algebra and/or Principles of Mathematics is desirable. |
| − | achieving superior results for | + | <br clear="all"> |
| − | discrete wavelet transformation techniques. | + | |
| − | The second student group will research the topic of image fusion. Fusing high resolution gray- | + | *[http://helmut.knaust.info/class/201330_NREUP/application_form.pdf Application form]. The application deadline is '''Friday, May 10, 2013'''. |
| − | scale satellite images with lower resolution multispectral images is of major interest to geographers | + | |
| − | using remote sensing, in particular to study food production. Some earlier fusion techniques did | + | *'''Project Director.''' [mailto:hknaust@utep.edu Helmut Knaust], Department of Mathematical Sciences, The University of Texas at El Paso, El Paso TX 79968. |
| − | not use wavelet techniques, but recently discrete wavelet transform methods have been successfully | + | |
| − | employed. The major idea is to replace certain portions of the transformed gray-scale image by | + | *'''Project Description.''' Five undergraduate students majoring in Mathematics will participate in an intensive six-week summer research program on wavelets. |
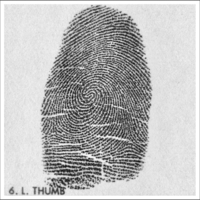
| − | corresponding portions of each channel of the transformed color image. The results are superior | + | **[[image:fingerprint.png|200px|left]]The first group of students will investigate whether the FBI fingerprint algorithm [1] can be adapted to other classes of similar images such as facial portraits. Historically the adoption by the FBI of a compression algorithm for storing fingerprints digitally was the first major "applied" success of the wavelet research community. The algorithm is derived from the general JPEG2000 compression algorithm, but cleverly exploits the special character of the images to be processed by selecting a particular wavelet package and quantization scheme, thereby achieving superior results for fingerprint compression compared to Fourier or more general-purpose discrete wavelet transformation techniques. <br clear="all"> |
| − | to those simply using resampling techniques for multi-spectral images. The students will study | + | **The second student group will research the topic of image fusion. Fusing high resolution gray-scale satellite images with lower resolution multispectral images is of major interest to geographers using remote sensing, in particular to study food production. Some earlier fusion techniques did not use wavelet techniques, but recently discrete wavelet transform methods have been successfully employed [2,3]. The major idea is to replace certain portions of the transformed gray-scale image by corresponding portions of each channel of the transformed color image. The results are superior to those simply using resampling techniques for multi-spectral images. The students will study various fusion techniques, try to find other possible replacement and implementation schemes, and investigate methods to compare the quality of fusion results. <br>[[image:Berlin_small.png|300px]] [[image:Berlin_gray.png|300px]] |
| − | various fusion techniques, try to | + | <br clear="all"> |
| − | investigate methods to compare the quality of fusion results. | + | |
| + | *'''Stipends'''. Students will receive a stipend of $3,700 for participation in the program; additionally they will receive a UTEP food allowance. Textbooks and other materials will be provided. Participants need to be U.S. citizens or permanent residents. | ||
| + | |||
| + | *'''Expectations'''. This is a full-time job: Students will devote at least 40 hours per week to the project. Participants may sign up for an independent study course during the summer if they wish to receive academic credit for the summer research experience, but will not take other summer courses. | ||
| + | |||
| + | *'''Week-by-week'''. The summer research experience will start on June 10, and will last six weeks until July 19. | ||
| + | **'''Weeks 1 and 2.''' Students will become familiar with the basics of discrete wavelet transformations by daily lectures and self-study. A suitable resource is van Fleet's undergraduate textbook [5]. Additionally, students will learn the basics of Mathematica by working on topic-related programming exercises. | ||
| + | **'''Week 3.''' Students will use ''Mathematica'' to implement the FBI fingerprint algorithm [4], and several fusion algorithms (e.g. [2] and [3]), respectively. | ||
| + | **'''Week 4 and 5.''' Students will engage in the research portion of the project extending the known results obtained in Week 3. | ||
| + | **'''Week 6.''' Students will prepare a poster of their research results, and write up their findings in a research report. | ||
| + | |||
| + | *'''Learning Outcomes'''. The following learning outcomes will result from the summer research experience. Participants will: | ||
| + | **get a taste of doing research in Mathematics. This will motivate and prepare them for participation in a graduate program in the Mathematical Sciences. | ||
| + | **get exposed to the methods and issues involved in applying mathematics to a relevant engineering problem. | ||
| + | **learn how to use a computer algebra system for mathematical investigations, as a computational and visualization aid, and for the implementation of mathematical algorithms. | ||
| + | **be able to give and defend a mathematical presentation to a group of their peers and the professional community. | ||
| + | **develop an understanding of the theoretical underpinnings of wavelet transforms and their applications. | ||
| + | |||
| + | *'''References.''' | ||
| + | #[http://helmut.knaust.info/class/201330_NREUP/spie93_Fingerprint.pdf J.N. Bradley, C.M. Brislawn, T. Hopper. The FBI Wavelet/Scalar Quantization Standard for gray-scale fingerprint image compression.] SPIE, Vol. 1961, Visual Information Processing II (1993), pp. 293-304. | ||
| + | #[http://helmut.knaust.info/class/201330_NREUP/Fingerprint1.pdf C.M. Brislawn, J.N. Bradley, et al. The FBI Compression Standard for Digitized Fingerprint Images.] Preprint, 1996. | ||
| + | #[http://helmut.knaust.info/class/201330_NREUP/LKW.pdf Shutao Li, James T. Kwok, Yaonan Wang. Using the discrete wavelet frame transform to merge Landsat TM and SPOT panchromatic images.] Information Fusion 3 (2002) pp. 17-23. | ||
| + | #[http://helmut.knaust.info/class/201330_NREUP/LJYS.pdf Zhenhua Li, Zhongliang Jing, Xuhong Yang, Shaoyuan Sun. Color transfer based remote sensing image fusion using non-separable wavelet frame transform.] Pattern Recognition Letters 26 (2005), pp. 2006-14. | ||
| + | #David K. Ruch & Patrick J. Van Fleet. Wavelet Theory: An Elementary Approach with Applications. Wiley (2010). | ||
| + | #Patrick J. Van Fleet. Discrete Wavelet Transformations. Wiley (2008). | ||
| + | |||
| + | ===Miscellaneous Information=== | ||
| + | *[http://www.maa.org/programs/faculty-and-departments/underrepresented-groups/nreup/university-of-texas-el-paso-2013 Program page at the MAA] | ||
| + | *Lectures, Week 2: 9-11 and 2-4 in the MarCS Conference Room. | ||
| + | *Lectures, Week 1: 9-11 in the MarCS Conference Room, 2-4 in Bell Hall 125. | ||
| + | *Student Offices: Bell Hall 220 and 318. | ||
| + | *Access ''Mathematica'' from anywhere: [[Mydesktop.utep.edu]] | ||
| + | *Project evaluator: [mailto:Gulden.Karakok@unco.edu Dr. Gulden Karakok] | ||
| + | *[http://helmut.knaust.info/class/201330_NREUP/SURME_2013.pdf SURME Summer Schedule] | ||
| + | |||
| + | ===Materials=== | ||
| + | * [https://photos.app.goo.gl/xLuKLvYjnSxLp3Qb7 Photos] | ||
| + | * [http://helmut.knaust.info/class/201330_NREUP/Presentation.pps Going to Graduate School in Mathematics] | ||
| + | * [http://faculty.washington.edu/robinet/poster.html How to Make a Poster Using PowerPoint], by Renee Robinette Ha | ||
| + | * [http://abacus.bates.edu/~bpfohl/posters/ Poster-making 101], by Brian Pfohl | ||
| + | * [[Assignments]] | ||
| + | * [http://helmut.knaust.info/class/201310_5311/Images.zip Images (zip file)] | ||
| + | * [http://helmut.knaust.info/class/201310_5311/Notebooks/ ''Mathematica'' Notebooks] | ||
| + | * [http://helmut.knaust.info/class/201310_5311/IntroDWT.pdf Introduction] | ||
| + | * [http://helmut.knaust.info/class/201310_5311/MRA.pdf Multi-Resolution Analysis for the Haar Wavelet] | ||
| + | * [http://www.mathematica25.com/ 1988-2013 - 25 Years of Mathematica] | ||
| + | * David A. Huffman. [http://compression.ru/download/articles/huff/huffman_1952_minimum-redundancy-codes.pdf ''A Method for the Construction of Minimum-Redundancy Codes.''] Proceedings of the I.R.E., September 1952, pp. 1098–1101. | ||
| + | |||
| + | ===Student Reports and Posters=== | ||
| + | ====Image Fusion Team==== | ||
| + | [[image:ImageFusionPoster.jpg|left]]<br clear=all> | ||
| + | * [http://helmut.knaust.info/class/201330_NREUP/ImageFusion.pdf Research Report] | ||
| + | * [http://helmut.knaust.info/class/201330_NREUP/ImageFusionPoster.pdf Poster] | ||
| + | |||
| + | ====Fingerprint Team==== | ||
| + | [[image:FingerprintPoster.jpg|left]]<br clear=all> | ||
| + | * [http://helmut.knaust.info/class/201330_NREUP/Fingerprint.pdf Research Report] | ||
| + | * [http://helmut.knaust.info/class/201330_NREUP/FingerprintPoster.pdf Poster] | ||
Latest revision as of 17:18, 8 January 2021
UTEP Summer Research Experience for Undergraduates: Applications of Discrete Wavelet Transformations
June 10 - July 19, 2013
Contents |
[edit] Program Description
The National Research Experience for Undergraduates Program (NREUP) is a program of the Mathematical Association of America, funded by the National Security Agency (H98230-13-1-0270) and the National Science Foundation (DMS-1156582).The target audience for the program are primarily sophomores and juniors majoring in Mathematics. Successful completion of Calculus II is required; successful completion of Matrix Algebra and/or Principles of Mathematics is desirable.
- Application form. The application deadline is Friday, May 10, 2013.
- Project Director. Helmut Knaust, Department of Mathematical Sciences, The University of Texas at El Paso, El Paso TX 79968.
- Project Description. Five undergraduate students majoring in Mathematics will participate in an intensive six-week summer research program on wavelets.
- The first group of students will investigate whether the FBI fingerprint algorithm [1] can be adapted to other classes of similar images such as facial portraits. Historically the adoption by the FBI of a compression algorithm for storing fingerprints digitally was the first major "applied" success of the wavelet research community. The algorithm is derived from the general JPEG2000 compression algorithm, but cleverly exploits the special character of the images to be processed by selecting a particular wavelet package and quantization scheme, thereby achieving superior results for fingerprint compression compared to Fourier or more general-purpose discrete wavelet transformation techniques.
- The second student group will research the topic of image fusion. Fusing high resolution gray-scale satellite images with lower resolution multispectral images is of major interest to geographers using remote sensing, in particular to study food production. Some earlier fusion techniques did not use wavelet techniques, but recently discrete wavelet transform methods have been successfully employed [2,3]. The major idea is to replace certain portions of the transformed gray-scale image by corresponding portions of each channel of the transformed color image. The results are superior to those simply using resampling techniques for multi-spectral images. The students will study various fusion techniques, try to find other possible replacement and implementation schemes, and investigate methods to compare the quality of fusion results.


- The first group of students will investigate whether the FBI fingerprint algorithm [1] can be adapted to other classes of similar images such as facial portraits. Historically the adoption by the FBI of a compression algorithm for storing fingerprints digitally was the first major "applied" success of the wavelet research community. The algorithm is derived from the general JPEG2000 compression algorithm, but cleverly exploits the special character of the images to be processed by selecting a particular wavelet package and quantization scheme, thereby achieving superior results for fingerprint compression compared to Fourier or more general-purpose discrete wavelet transformation techniques.
- Stipends. Students will receive a stipend of $3,700 for participation in the program; additionally they will receive a UTEP food allowance. Textbooks and other materials will be provided. Participants need to be U.S. citizens or permanent residents.
- Expectations. This is a full-time job: Students will devote at least 40 hours per week to the project. Participants may sign up for an independent study course during the summer if they wish to receive academic credit for the summer research experience, but will not take other summer courses.
- Week-by-week. The summer research experience will start on June 10, and will last six weeks until July 19.
- Weeks 1 and 2. Students will become familiar with the basics of discrete wavelet transformations by daily lectures and self-study. A suitable resource is van Fleet's undergraduate textbook [5]. Additionally, students will learn the basics of Mathematica by working on topic-related programming exercises.
- Week 3. Students will use Mathematica to implement the FBI fingerprint algorithm [4], and several fusion algorithms (e.g. [2] and [3]), respectively.
- Week 4 and 5. Students will engage in the research portion of the project extending the known results obtained in Week 3.
- Week 6. Students will prepare a poster of their research results, and write up their findings in a research report.
- Learning Outcomes. The following learning outcomes will result from the summer research experience. Participants will:
- get a taste of doing research in Mathematics. This will motivate and prepare them for participation in a graduate program in the Mathematical Sciences.
- get exposed to the methods and issues involved in applying mathematics to a relevant engineering problem.
- learn how to use a computer algebra system for mathematical investigations, as a computational and visualization aid, and for the implementation of mathematical algorithms.
- be able to give and defend a mathematical presentation to a group of their peers and the professional community.
- develop an understanding of the theoretical underpinnings of wavelet transforms and their applications.
- References.
- J.N. Bradley, C.M. Brislawn, T. Hopper. The FBI Wavelet/Scalar Quantization Standard for gray-scale fingerprint image compression. SPIE, Vol. 1961, Visual Information Processing II (1993), pp. 293-304.
- C.M. Brislawn, J.N. Bradley, et al. The FBI Compression Standard for Digitized Fingerprint Images. Preprint, 1996.
- Shutao Li, James T. Kwok, Yaonan Wang. Using the discrete wavelet frame transform to merge Landsat TM and SPOT panchromatic images. Information Fusion 3 (2002) pp. 17-23.
- Zhenhua Li, Zhongliang Jing, Xuhong Yang, Shaoyuan Sun. Color transfer based remote sensing image fusion using non-separable wavelet frame transform. Pattern Recognition Letters 26 (2005), pp. 2006-14.
- David K. Ruch & Patrick J. Van Fleet. Wavelet Theory: An Elementary Approach with Applications. Wiley (2010).
- Patrick J. Van Fleet. Discrete Wavelet Transformations. Wiley (2008).
[edit] Miscellaneous Information
- Program page at the MAA
- Lectures, Week 2: 9-11 and 2-4 in the MarCS Conference Room.
- Lectures, Week 1: 9-11 in the MarCS Conference Room, 2-4 in Bell Hall 125.
- Student Offices: Bell Hall 220 and 318.
- Access Mathematica from anywhere: Mydesktop.utep.edu
- Project evaluator: Dr. Gulden Karakok
- SURME Summer Schedule
[edit] Materials
- Photos
- Going to Graduate School in Mathematics
- How to Make a Poster Using PowerPoint, by Renee Robinette Ha
- Poster-making 101, by Brian Pfohl
- Assignments
- Images (zip file)
- Mathematica Notebooks
- Introduction
- Multi-Resolution Analysis for the Haar Wavelet
- 1988-2013 - 25 Years of Mathematica
- David A. Huffman. A Method for the Construction of Minimum-Redundancy Codes. Proceedings of the I.R.E., September 1952, pp. 1098–1101.