Assignments
From Classes
Revision as of 19:11, 13 June 2013 by HelmutKnaust (Talk | contribs)
- \(\checkmark\) Let \(A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&10\end{pmatrix}\). Find a matrix X such that \(X\cdot A=\begin{pmatrix}7&8&10\\4&5&6\\1&2&3\end{pmatrix}\). What do you get if you compute \(A\cdot X\)?
- Find a 4x4 orthogonal matrix with at least 5 non-zero entries.
- Can you find a 3x3 orthogonal matrix with no zeroes? Notebook
- \(\checkmark\) Find the vertical edges of a grayscale image (of your choice). Hint: For horizontal edges this is done in Notebook 031.
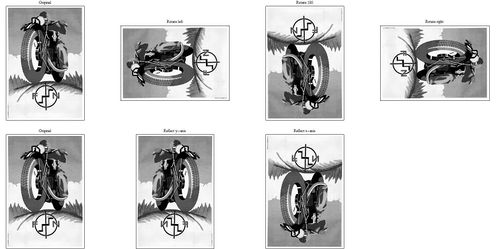
- \(\checkmark\) Pick a small grayscale image (your choice) and use matrix transposition and multiplication with suitable matrices to produce the following six images:
- In Notebook 032 you have seen how to convert a color image to its YCbCr components. Recreate the original color image from its Y-, Cb- and Cr- components. (Check your result by computing the Peak Signal to Noise Ratio to the original image. Note that when computing the luminance/chrominance components, we round to the nearest integer. )
- Problem 3.8
- Problem 3.16
- Problem 3.23
- Problem 3.26
- Problem 3.35
- Problem 3.37
- Problem 3.40
- Problem 3.42
- Compute the real and/or complex Fourier series for the functions \(f(t)=t\) or \(f(t)=|t|\).