Assignments
From Classes
Revision as of 08:49, 11 June 2013 by HelmutKnaust (Talk | contribs)
- Let \(A=\begin{pmatrix}1&2&3\\4&5&6\\7&8&10\end{pmatrix}\). Find a matrix X such that \(X\cdot A=\begin{pmatrix}7&8&10\\4&5&6\\1&2&3\end{pmatrix}\). What do you get if you compute \(A\cdot X\)?
- Find a 4x4 orthogonal matrix with at least 5 non-zero entries.
- Can you find a 3x3 orthogonal matrix with no zeroes? Notebook
- Find the horizontal edges of a grayscale image (of your choice). Hint: For vertical edges this is done in Notebook 031.
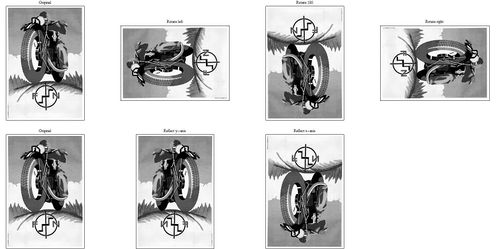
- Pick a small grayscale image (your choice) and use matrix transposition and multiplication with suitable matrices to produce the following six images:
- Problem 3.8
- Problem 3.16