Homework 1 - Introduction to Analysis - Fall 97

The problems are due on September 11.

Problem 1. Show that is irrational.

Problem 2. A set A of real numbers is called bounded, if there are , so that for all . Show that the following statements are equivalent:

1. Every non-empty bounded set has an infimum and a supremum.
2. Every non-empty set, which is bounded from below, has an infimum.
3. Every non-empty set, which is bounded from above, has a supremum.

Problem 3. Let . Show that A is bounded from above in , but has no least upper bound in .

Hint. One of the steps in the proof is to show the following: If and r>0, choose a rational number q such that 0<q<1 and 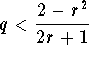. Show that .

Problem 4. Let A be a non-empty set, which is bounded from above. Show: If , then for all , there is an with .

Problem 5. Prove the correct statement, and give a counterexample to the incorrect one:

1. If the sequence converges to |a|, then the sequence converges to a.
2. If the sequence converges to a, then the sequence converges to |a|.