Homework 2 - Introduction to Analysis - Fall 97

The problems are due on September 25. This is a group assignment. Turn in only one solution per group.

The first three problems deal with constructing the real numbers from the rational numbers.

Let's denote the set of all Cauchy sequences of rational numbers by tex2html_wrap_inline112 . We say that two Cauchy sequences tex2html_wrap_inline114 and tex2html_wrap_inline116 of rational numbers are equivalent, if tex2html_wrap_inline118 . If two Cauchy sequences tex2html_wrap_inline114 and tex2html_wrap_inline116 are equivalent, we write tex2html_wrap_inline124 .

Problem 1. Show that tex2html_wrap_inline126 is indeed an equivalence relation, i.e, show for all tex2html_wrap_inline128 and tex2html_wrap_inline130 :
  1. tex2html_wrap_inline132 (Reflexivity)
  2. tex2html_wrap_inline134 (Symmetry)
  3. tex2html_wrap_inline124 and tex2html_wrap_inline138 (Transitivity)
An equivalence class tex2html_wrap_inline140 is the set of all Cauchy sequences of rational numbers equivalent to tex2html_wrap_inline142 :

displaymath104

Note that tex2html_wrap_inline144 if and only if tex2html_wrap_inline146 .

We denote the set of all such equivalence classes by tex2html_wrap_inline148 . tex2html_wrap_inline148 can be considered as a model for the set of real numbers. (To every equivalence class in tex2html_wrap_inline148 there corresponds in a unique way a real number: The real number associated with tex2html_wrap_inline154 is its limit . In particular, an equivalence class tex2html_wrap_inline158 represents a rational number if and only if tex2html_wrap_inline142 is equivalent to a constant sequence.)

From now on we will call the elements of tex2html_wrap_inline148 real numbers.

We define addition tex2html_wrap_inline164 and multiplication tex2html_wrap_inline166 of real numbers as follows:

displaymath105

Subtraction tex2html_wrap_inline168 and division tex2html_wrap_inline170 are defined similarly.

Problem 2.
  1. Show that the addition tex2html_wrap_inline164 is well-defined. (You have to show two things. First establish that the sum of two Cauchy sequences is Cauchy, then show: if tex2html_wrap_inline174 and tex2html_wrap_inline176 , then tex2html_wrap_inline178 .)
  2. One can similarly show that the multiplication tex2html_wrap_inline166 is well-defined. Show that the multiplication tex2html_wrap_inline166 is commutative and associative. Find the neutral element with respect to multiplication in tex2html_wrap_inline148 .
  3. Show the distributive law

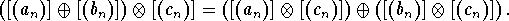
    displaymath106

We say tex2html_wrap_inline158 is positive, if there are a rational number tex2html_wrap_inline188 and tex2html_wrap_inline190 so that tex2html_wrap_inline192 for all tex2html_wrap_inline194 . We then define an order tex2html_wrap_inline196 on tex2html_wrap_inline148 as follows:

displaymath107

Problem 3.
  1. Show that the order tex2html_wrap_inline196 is well-defined.
  2. Show that the order tex2html_wrap_inline196 is transitive.
  3. Show that tex2html_wrap_inline204 implies tex2html_wrap_inline206 for all tex2html_wrap_inline208 and tex2html_wrap_inline210 .
  4. Show for any real number tex2html_wrap_inline158 : Either tex2html_wrap_inline158 is positive, tex2html_wrap_inline216 is positive, or tex2html_wrap_inline158 is the equivalence class of the sequence, which is constantly 0.
By now, you have established about half of the axioms defining an ordered field, and in fact, tex2html_wrap_inline148 is an ordered field. What about the completeness axiom? With considerably more effort and using an appropriate set of axioms for the natural numbers, one can indeed show that with this definition the real numbers satisfy the completeness axiom.

Problem 4. p. 59, #39

Problem 5. p. 59, #31

Helmut Knaust
Thu Sep 11 11:08:28 MDT 1997