Homework 3 - Introduction to Analysis - Fall 97

The problems are due on October 9. This is an individual assignment.

Problem 1. Prove or disprove the following statements:

1. If x is an accumulation point of 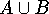, then x is an accumulation point of A, or x is an accumulation point of B.
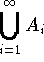2. If x is an accumulation point of , then there is an 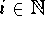so that x is an accumulation point of .
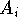3. If x is an accumulation point of A and x is an accumulation point of B, then x is an accumulation point of .

Problem 2. Prove the following: If 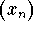is a sequence so that 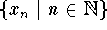has at least two accumulation points, then 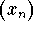diverges.

Problem 3. A sequence 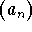is called proper, if 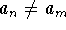for all .

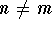1. Show that a proper bounded sequence converges, if 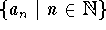has exactly one accumulation point.
2. Show that 1. fails if we omit the hypothesis that the sequence is bounded.
3. Show that 1. fails if we omit the hypothesis that the sequence is proper.

Problem 4. Let 0<r<1 and let 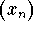be a sequence satisfying

for all 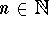. Show that 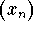converges!

Problem 5. Let 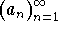be a Cauchy sequence, and let 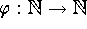be any 1-1 function. Show that the sequence 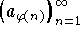is Cauchy.