Math 4111
Test 3
Spring 1996
No books, notes etc. are permitted.
Show all your work! Box in your answers!
The test has 7 problems on 4 pages.
Read the problems carefully!
Problem 2 (15 points)
- 1.
- Find the first three derivatives of
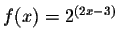 .
.
- 2.
- Find the 100th derivative of
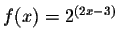 .
.
Problem 3 (10 points)
Find an equation for the tangent line of
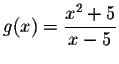 at x
at x=0
.
Problem 4 (10 points)
Let
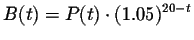 . Given that P
. Given that P(8)=120
and P'(8)=6
, find B'(8)
.
Problem 5 (15 points)
A 300 feet tall hotel has an elevator on the outside of the building. You are standing by a window 100 feet above the ground and 150 feet away from the hotel, and the elevator descends from the top of the hotel at a constant speed of 20 feet per second, starting at time t=0
, where t is measured in seconds. Let  be the angle between the line of your horizon and your line of sight of the elevator.
be the angle between the line of your horizon and your line of sight of the elevator.
- 1.
- Find a formula for h(t), the elevator's height above ground, as it descends from the top of the hotel.
- 2.
- Express
 as a function of time t.
as a function of time t.
- 3.
- If the rate of change of
 with respect to time t is a measure of how fast the elevator appears to you to be moving, at what height will the elevator be when it appears to be moving the fastest?
with respect to time t is a measure of how fast the elevator appears to you to be moving, at what height will the elevator be when it appears to be moving the fastest?
Problem 6 (15 points)
Find the quantity
 at the point
at the point (8,8)
on the curve
x2/3+y2/3=8.
Helmut Knaust
1999-02-02
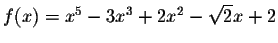
![$\displaystyle f(x)=[\sin(x)]^2 \cdot \cos(x) $](img3.gif)
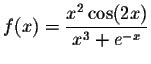
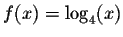
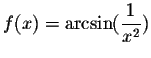
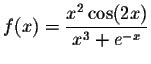
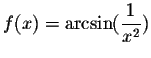
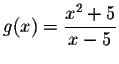 at x=0.
at x=0.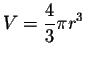 .)
.)