CRN 16078
From Classes
(Difference between revisions)
HelmutKnaust (Talk | contribs) (→Written Homework) |
HelmutKnaust (Talk | contribs) (→Materials) |
||
| (17 intermediate revisions by one user not shown) | |||
| Line 27: | Line 27: | ||
===Written Homework=== | ===Written Homework=== | ||
| − | *[http://helmut.knaust.info/class/201910_4341/HW03.pdf Homework 3, due 9/27] | [http://helmut.knaust.info/class/201910_4341/HW02.pdf Homework 2, due 9/20] | [http://helmut.knaust.info/class/201910_4341/HW01.pdf Homework 1, due 9/11] | + | *[http://helmut.knaust.info/class/201910_4341/HW07.pdf Homework 7, due 12/4] | [http://helmut.knaust.info/class/201910_4341/HW06.pdf Homework 6, due 11/6] | [http://helmut.knaust.info/class/201910_4341/HW05.pdf Homework 5, due 10/25] | [http://helmut.knaust.info/class/201910_4341/HW04.pdf Homework 4, due 10/16] | [http://helmut.knaust.info/class/201910_4341/HW03.pdf Homework 3, due 9/27] | [http://helmut.knaust.info/class/201910_4341/HW02.pdf Homework 2, due 9/20] | [http://helmut.knaust.info/class/201910_4341/HW01.pdf Homework 1, due 9/11] |
===Materials=== | ===Materials=== | ||
| − | *[http://www.cds.caltech.edu/~marsden/volume/eca/2000/ECA_errata_10-16-00.pdf Errata for early printings of the second edition of the textbook] | [http://helmut.knaust.info/class/201910_4341/Errata10.pdf Errata for late printings of the second edition of the textbook] | + | * [https://www.jstor.org/stable/2301999 A simple continuous function with a finite derivative at no point], by T.H. Hildebrandt (1933) | [http://helmut.knaust.info/class/201910_4341/EulerBL.nb Euler's Broken Line (Mathematica)] | [http://web.stanford.edu/~jluk/math63CMspring17/Existence.170408.pdf Notes on Existence and Uniqueness Theorems for ODEs], by Jonathan Luk. | [http://helmut.knaust.info/class/201910_4341/NoDiff.nb A nowhere differentiable continuous function (Mathematica)] | [http://helmut.knaust.info/class/201910_4341/FTALang.pdf D'Alembert's proof of the Fundamental Theorem of Algebra], by Serge Lang | [http://helmut.knaust.info/class/201510_3341/Check_and_Greek.pdf How to Check Proofs, etc.] | [http://www.cds.caltech.edu/~marsden/volume/eca/2000/ECA_errata_10-16-00.pdf Errata for early printings of the second edition of the textbook] | [http://helmut.knaust.info/class/201910_4341/Errata10.pdf Errata for late printings of the second edition of the textbook] |
Latest revision as of 14:07, 6 December 2018
[edit] Syllabus
- Time and Place. TR 17:00-18:20, LART 308
- Instructor. Helmut Knaust, Bell Hall 219, hknaust@utep.edu, 747-7002
- Office Hours. TR 15:00-16:20, or by appointment.
- Textbook. Jerrold E. Marsden & Michael J. Hoffman, Elementary Classical Analysis, 2nd ed., W.H. Freeman and Co., New York.
- Prerequisites. MATH 3341 (Introduction to Analysis), or equivalent. The prerequisite material can be found for instance in: Edward D. Gaughan, Introduction to Analysis, American Mathematical Society; 5th revised edition, Ch. 0-5.
- Course Content. We will study the concept of a metric space. The rational numbers are dense in the set of real numbers: for every real number we can find a rational number arbitrarily close. If we want to consider the related question, whether and in what sense polynomials are dense in the set of continuous functions, we are naturally led to the general concept of the distance between two mathematical objects. A set with a distance function is called a metric space. In the first part of the course, you will learn about basic properties metric spaces might have, such as compactness, completeness and connectedness. As one of the most important examples of metric spaces we will then study the space of continuous functions with its notion of uniform convergence. One of the highlights of the course will be the proof of the Stone-Weierstrass-Theorem, which generalizes the result about polynomials mentioned above.
- Homework. You will be regularly assigned written homework problems, which will be spot-graded. Graduate students will be required to work on some extra problems. Your homework grade will contribute 15% towards your grade.
- Tests. The two midterms will take place on Tuesday, October 2 and Thursday, November 8, respectively. The final on Tuesday, December 11, 16:00-18:45, is mandatory and comprehensive. The midterm exams will each count 25%, and the final 35%.
- Time Requirement. I expect that you spend an absolute minimum of six hours a week outside of class on reading the textbook, preparing for the next class, reviewing your class notes, and completing homework assignments. Not surprisingly, it has been my experience that there is a strong correlation between class grade and study time.
- Attendance. You are strongly encouraged to attend class. Students with six absences (excused or unexcused) will be dropped from the course with a grade of "F".
- Drop Policy. The class schedule lists Friday, November 2, as the last day to drop with an automatic "W". After the deadline, I can only drop you from the course with a grade of "F".
- Students with Disabilities. If you have a disability and need classroom accommodations, please contact The Center for Accommodations and Support Services (CASS) at 747-5148, or by email to cass@utep.edu, or visit their office located in UTEP Union East, Room 106. For additional information, please visit the CASS website at www.utep.edu/student-affairs/cass/.
- Academic Integrity. All students must abide by UTEP's academic integrity policies, see the Academic Integrity and Scholastic Dishonesty section of the website of the Office for Student Conduct and Conflict Resolution at www.utep.edu/student-affairs/osccr/. Please note that you may not leave the classroom during an exam.
[edit] Written Homework
- Homework 7, due 12/4 | Homework 6, due 11/6 | Homework 5, due 10/25 | Homework 4, due 10/16 | Homework 3, due 9/27 | Homework 2, due 9/20 | Homework 1, due 9/11
[edit] Materials
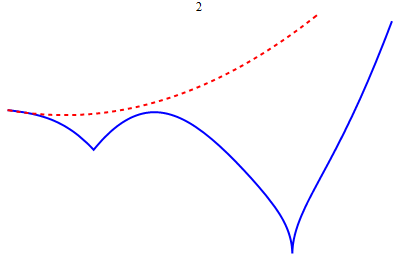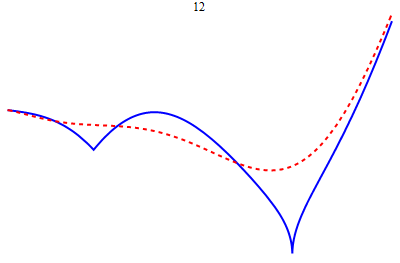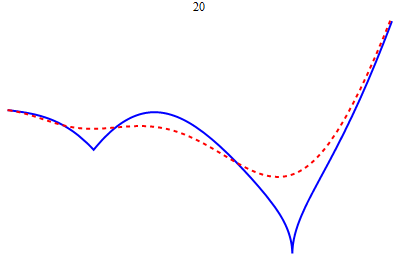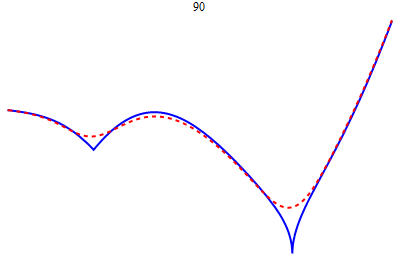
- A simple continuous function with a finite derivative at no point, by T.H. Hildebrandt (1933) | Euler's Broken Line (Mathematica) | Notes on Existence and Uniqueness Theorems for ODEs, by Jonathan Luk. | A nowhere differentiable continuous function (Mathematica) | D'Alembert's proof of the Fundamental Theorem of Algebra, by Serge Lang | How to Check Proofs, etc. | Errata for early printings of the second edition of the textbook | Errata for late printings of the second edition of the textbook